搞了一天的一道题 冷静一下了
Cliquers Strike Back [A]
Memory limit: 32 MB
An undirected graph is called a labeled cliquer if each connected component of the graph is a clique and the vertices of the graph are numbered with numbers from the set  . Maurycy has drawn all labeled cliquers with
. Maurycy has drawn all labeled cliquers with  vertices on a piece of paper and is going to assess beauty of each of them with a number from the set
vertices on a piece of paper and is going to assess beauty of each of them with a number from the set  (in particular, different cliquers may be assigned equal grades). In how many ways can he do this? The result should be computed modulo
(in particular, different cliquers may be assigned equal grades). In how many ways can he do this? The result should be computed modulo  . The figure below depicts all labeled cliquers for
. The figure below depicts all labeled cliquers for  .
.

Input
The only line of the standard input contains two integers  and
and  (
( ), separated by a single space and denoting the number of vertices of each labeled cliquer and the number of grades respectively.
), separated by a single space and denoting the number of vertices of each labeled cliquer and the number of grades respectively.
Output
The only line of the standard output should contain the number of possible sets of grades modulo  .
.
Example
For the input data:
3 2
the correct result is:
32
Task author: Tomasz Idziaszek.
n,m好大 查百度 看到Touchard同余
然后想到用类似算子的思想算x^n mod (x^p - x - 1) 类似快速幂
分解了一下phi 有两个几千大小的质数 然后用crt合并就行了
多项式取模怎么办呢? 想了一下On就行了
问题就是多项式乘法了 但是fft不靠谱 难道用分治乘?
写一个样例都T了
然后问杜教 杜教告诉我 Bn+p^k也是可以推的 我居然没有发现(原来维基上就有这个公式)
Modular arithmetic[edit]
The Bell numbers obey Touchard's congruence: If p is any prime number then[11]
or, generalizing[12]
然后杜教说是记忆化搜索
但我感觉状态数太多了
然后发现既然Bp^k=B+k 那么 Bn=B^(a0+a1p+a2p^2+a3p^3+..)=B^a0 * (B+1)^a1 * (B+2)^a2 * ...
现在只要做一点点多项式乘法了
但是还是T了一些
怎么办
然后我把原来1*x^a0用分治乘给写的去掉了
继续又把原来x^a0*(x+1)^a1用分治乘给写的去掉了
然后居然还T了一个点
然后我发现预处理比分治乘慢 然后我把预处理的取模去掉一个
然后居然A了
这道题真的一定要分治乘吗??????
附上同余式证明:
Let as write the Touchard's congruence as:
B(n) = B(n - (p - 1)) + B(n - p) (mod p), p prime
Take a set A of n elements, a subset B of p elements and T a cyclic
permutation of the p elements. Then, T^p = I (identity) and T^k =/= I, for
1 < k < p.
Then, the partitions of A can be clasified in three categories:
i) Partitions with the elements of B in a unique subset. They are invariants
under T and there are B(n - (p - 1))
ii) Partitions with each element of B in a subset of only one element. They
are invariants under T and there are B(n - p).
iii) The rest of partitions can be classified in h equivalence classes
(orbits) by aplication of T, each one of them with p partitions.
Then,
B(n) = B(n - (p - 1)) + B(n - p) + h*p ===> Touchard's congruence
-------原来xyz的PA选讲里就有这道题?!记忆化搜索真的能过?!
-------原来之前用欧拉五边形定理做的也能用别的方法搞?!!!?!!

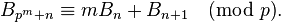
2015年5月12日 14:13
渣将,哥两次多余的分治乘没去掉都比你跑得快。。
太差了。。
2015年5月12日 14:34
我是马泽圣 我叼 !
2022年8月15日 22:35
Uttarakhand Board Model Paper 2023 Class 2 Pdf Download with Answers for English Medium, Hindi Medium, Urdu Medium & Students for Small Answers, Long Answer, UBSE Question Paper Class 2 Very Long Answer Questions, and Essay Type Questions to Term1 & Term2 Exams Uttarakhand Board Model Paper 2023 Class 2 Pdf Download with Answers for English Medium, Hindi Medium, Urdu Medium & Students for Small Answers, Long Answer, Very Long Answer Questions, and Essay Type Questions to Term1 & Term2 Exams